Hackle's blog
between the abstractions we want and the abstractions we get.

about

Also on Comonad and Conway's game of life

One way to get an intuition for Comonad, is to see it as a context with a focus. Good examples are Conway's game of life, calculating blur effect on a image, or "You Are The Average Of The Five People You Spend The Most Time With", or, what we can start with, "Passing the ball in a circle".

Passing the ball in a circle, Comonad in JavaScript

We want to write a program to record how a group of football players training together by passing the ball in a circle. It goes as "A passes the ball to B, B passes the ball to C ... E passes the ball to A, A passes the ball to B ...", you get the idea.

I am sure you can think of a good solution already but let's say the requirement is to use Comonad, so we need to find the context and the focus.

The example should be straightforward here - context is the group of players, A, B, C, D and E, and the focus is the index to the current player with the ball. With this in mind, we come to this nonchalant attempt in JavaScript, with some explicit naming.

const players = [ 'A', 'B', 'C', 'D', 'E' ];
const passes = players.map((currentPlayer, focus, context) => `${currentPlayer} passes the ball to ${context[(focus + 1) % context.length]}`);

console.log(passes.join(', '));

This is almost a Comonad! We have both context and focus. But not quite - a Comonad instance really needs to encapsulate the focus, which brings us to the the Haskell version here using NonEmpty.

players = fromList $ cycle [ 'A' .. 'E' ]

makePass :: NonEmpty Char -> String
makePass (a :| b : _) = a : " passes the ball to " ++ [ b ]

passes = extend makePass players

Do you see the focus of NonEmpty? It's a bit hidden - as the "head" element. A neat trick.

Now let's look at extend which comes with any Comonad instance. Doesn't it look awfully similar to map?

extend  :: (w a -> b) -> w a -> w b
map     :: (a   -> b) -> w a -> w b

Note how the mapper function (w a -> b) of extend takes the entire w a, or, the context as the argument for mapping to b. Without an index to find each a with, we must build a different w a with its own focus for (w a -> b) to do the mapping. That's exactly what duplicate does.

> import Control.Comonad
> import Data.List.NonEmpty
Control.Comonad Data.List.NonEmpty> duplicate $ 'A' :| ['B'..'E']
('A' :| "BCDE") :| ['B' :| "CDE",'C' :| "DE",'D' :| "E",'E' :| ""]

It builds a list of lists, with the "head" moving towards the "tail" for each list. Remember, "head" is the focus of the list. This gives rise to makePass, which you would have noticed, is the mapper function (w a -> b).

Incidentally, we also use cycle to build an infinite list so there is always the next 2 players for passing the ball (from and to). But be warned a cycled list won't stop printing in GHCI if you try.

Comonad and Conway's game of life

It may seem the Conway's game of life is much more complex than "passing the ball", but it's actually not!

Now that we know extend is much like map, while the latter projects each element directly, extend projects the context w a. This alone makes extend a good match for Conway's game of life, where we'll remember, each cell dies or lives depending on its context (in the form of neighbouring cells).

Also now we know w a encapsulates a focus, so each call to (w a -> b) can result in a different b (or the same b if so desired). To build a w a for each element a, we implement either duplicate or extend.

You'll see the intuition of context and focus are paying off. There is still the elephant in the room - "passing the ball" deals with a list indexed by integers, but Conway's game of life needs a matrix, indexed by coordinates. Hardly a show stopper.

Thus my solution to Conway's game of life which should hopefully look straightforward by now.

type Coord = (Int, Int)
data Game a = Game { 
    coords :: Matrix a
    , focus :: Coord 
    } deriving (Functor, Show)

instance Comonad Game where
    extract (Game coords (r, c))= getElem r c coords
    duplicate g@(Game coords focus) = Game games focus where
        games = mapPos makeOne coords
        makeOne p _ = Game coords p

rule :: Game Bool -> Bool
rule g@(Game coords (r, c)) = liveNbrs == 3 || (isAlive && liveNbrs == 2) where
    isAlive = extract g
    liveNbrs = length $ filter id neighbours
    neighbours = isAliveOne <$> neighbourCoords `at` (r, c)
    isAliveOne (r, c) = maybe False id $ safeGet r c coords

Just to iterate on the above points,

• Game encapsulates a matrix
• the focus is an index into the matrix
• duplicate builds a matrix of Game each focusing on its own index
• rule takes advantage of Game as the context to calculate the total of live neighbouring cells

Sexiness for nothing?

The discerning reader would have noticed we don't really need the sexiness of Comonad for Conway's game of life either, much like passing the football, we just need a map for matrix, and it's indeed handy. I'll leave it to you to figure out an implementation - it can be (even) less hassle than the Haskell version.

Of course, Comonad as an abstraction can be much more powerful than just encapsulating an index in a list/matrix. There are more interesting instances such as Store or ZipperList as can be found in the "reference" section below.

References

I first heard the idea of using Comonad for Conway's game of life casually mentioned in this highly-recommended video by the good Bartosz, then I found this implementations by Dan Oneață with Store, more impressively Representable Store by Chris Penner, and Zippers by Samuel Gélineau.

The Zippers is a mind bender and totally did my head in. The plain Store features conceptual clarity but suffers from performance penalty. It's better with Representable Store which has to represent Vector that is not itself representable (warning: Category Theory mumbo), and I couldn't help wondering if it can be made more intuitive.

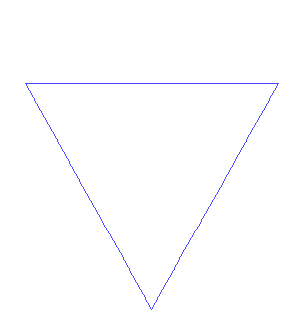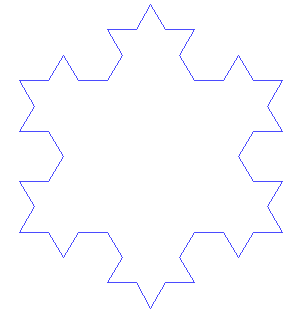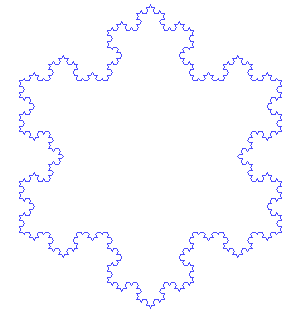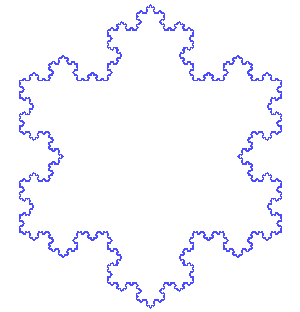
After staring at extract :: w a -> a and duplicate :: w a -> w (w a) long enough, I somehow find the intuition resemble that of fractals, for example Koch's snowflake (from Wikipedia). Be warned this might not be right for you.

Also beware, duplicate usually only goes one level down (or else my head explodes) but I found the intuition helpful.

Of course, the risk of being specific with any example for anything Haskell or Category Theory, is no example can fulfill the whole abstraction. So once you get an intuition with context and focus (as far as they can take us!) but before stretching them to the breaking point, it's best to accept Comonad as it comes - (w a) -> w (w a), no more, no less.